Intrinsic Features of Blobs

From FarsightWiki
(Difference between revisions)
Jump to: navigation, search
(→Features)
 
(14 intermediate revisions by 2 users not shown)
Line 1: Line 1:
−
== Intrinsic Features for Blobs ==
 
 
These features can be calculated with two input images (Data Image and Label Image).  
 
These features can be calculated with two input images (Data Image and Label Image).  
 
They are most commonly used for blob-like regions, such as cell nuclei.
 
They are most commonly used for blob-like regions, such as cell nuclei.
 +
Equations are shown for 3-dimensional space unless otherwise noted.
  
−
===''Volume''===
+
== Glossary of Notation ==
−
Number of voxels in the object. (Dirk)
+
{| border="1px" cellpadding="3" style="text-align:left"
−
===''Integrated Intensity''===
+
|-
−
Sum of the intensities of all voxels in the object. (Dirk)
+
| <math>p=(x,y,z)</math>
−
===''Centroid (unweighted and weighted)''===
+
| the coordinate of a voxel (three-dimensional point in a volume image)
−
The unweighted centroid calculates the center of the object.
+
|-
−
The weighted centroid uses the image intensity values to calculate the intensity center of the object. (Dirk)
+
| <math>N_p</math>
−
===''Axes Lengths''===
+
| a neighbor voxel of <math>p</math>
−
The length of the axes of the ND hyper-ellipsoid fit to the object. (Dirk)
+
|-
−
===''Eccentricity''===
+
| <math>l_p</math>
−
Ratio of the distance between the foci of the best-fit hyper-ellipsoid to the length of its major axis. (2D) (Dirk)
+
| the segmentation label at <math>p</math>
−
===''Elongation''===
+
|-
−
Ratio of the major axis length to minor axis length of the best-fit hyper-ellipsoid. (2D) (Dirk)
+
| <math>I_i(p)</math>
−
===''Orientation''===
+
| the intensity value of <math>p</math> at <math>i^{th}</math>
−
Angle between the major axis of the best-fit hyper-ellipsoid and origin. (2D) (Dirk)
+
|-
−
===''Bounding Box Volume''===
+
| <math>\Omega = \{p|l_p = o\}</math>
−
Number of voxels in the bounding box of the object. (Dirk)
+
| the set of voxels of an object <math>o</math>
−
===''Oriented Bounding Box Volume''===
+
|-
−
Number of voxels in the oriented bounding box of the object.
+
| <math>\Omega_s = \{l_p = o; \exists N_p, l_{N_p} \neq o\}</math>
−
The oriented bounding box is defined as the bounding box aligned along the axes of the object. (Dirk)
+
| the set of surface voxels of the object
−
===''Sum''===
+
|-
−
Same as integrated intensity (ITK statistics)
+
| <math>\Omega_{in} = \Omega - \Omega_s</math>
−
===''Mean''===
+
| the set of interior voxels of an object
−
Average intensity of voxels in the object (ITK statistics)
+
|-
−
===''Median''===
+
| <math>\overline{p}</math>
−
Middle intensity of voxels in the object (ITK statistics)
+
| the center of mass of the object
−
===''Minimum''===
+
|-
−
Minimum intensity of voxels in the object (ITK statistics)
+
| <math>P(I)</math>
−
===''Maximum''===
+
| Probability Density Function (PDF) of intensity values <math>I</math>
−
Maximum intensity of voxels in the object (ITK statistics)
+
|-
−
===''Sigma''===
+
| <math>M_{p,q,r} = \sum_{z=0}^{Z-1}\sum_{y=0}^{Y-1}\sum_{x=0}^{X-1}x^p y^q z^r I(x,y,z)</math>
−
Standard deviation of intensity of voxels in the object (ITK statistics)
+
| Raw Moment of discrete image <math>I</math>
−
===''Variance''===
+
|-
−
Variance of intensity of voxels in the object (ITK statistics)
+
| <math>\lambda_i</math>
−
===''Radius Variation''===
+
| <math>i^{th}</math> eigenvalue of covariance matrix
−
Standard deviation of distance from surface voxels to centroid (Isaac)
+
|-
−
===''Skew''===
+
| <math>\overline{v_i}</math>
−
Skew of the normalized intensity histogram (Isaac) (See Supplement B2)
+
| eigenvector corresponding to <math>\lambda_i</math>
−
===''Energy''===
+
|}
−
Energy of the normalized intensity histogram (Isaac) (See Supplement B2)
+
−
===''Entropy''===
+
−
Entropy of the normalized intensity histogram (Isaac) (See Supplement B2)
+
−
===''Surface Gradient''===
+
−
Average of surface gradients (Isaac)
+
−
===''Interior Gradient''===
+
−
Average of interior gradients (Isaac)
+
−
===''Interior Intensity''===
+
−
Average of interior intensities (Isaac)
+
−
===''Surface Intensity''===
+
−
Average of surface intensities (Isaac)
+
−
===''Intensity Ratio''===
+
−
Ratio of surface intensity to interior intensity (Isaac)
+
−
===''Shared Boundary''===
+
−
Ratio of surface area that touches another object to total surface area (Isaac)
+
−
===''Surface Area''===
+
−
Number of voxels on surface of the object (Isaac)
+
−
===''Shape''===
+
−
Ratio of surface voxels to total voxels - compactness or thinness of object (Isaac) (See Supplement B2)
+
  
−
==Glossary of Notation==
+
== Features ==
−
<FONT SIZE="+1"><math>p=(x,y,z)</math></FONT> - the coordinate of a voxel (three-dimensional point in a volume image)<br />
+
{| border="1px" cellpadding="3" style="text-align:left"
−
<FONT SIZE="+1"><math>N_p</math></FONT> - a neighbor voxel of <math>p</math><br />
+
|-
−
<FONT SIZE="+1"><math>l_p</math></FONT> - the segmentation label at <math>p</math><br />
+
| '''Name'''
−
<FONT SIZE="+1"><math>I_i(p)</math></FONT> - the intensity value of <math>p</math> at <math>i^{th}</math> channel<br />
+
| '''Units'''
−
<FONT SIZE="+1"><math>\Omega = \{p|l_p = o\}</math></FONT> - the set of voxels of an object <math>o</math><br />
+
| '''Description'''
−
<FONT SIZE="+1"><math>\Omega_s = \{l_p = o; \exists N_p, l_{N_p} \neq o\}</math></FONT> - the set of surface voxels of the object<br />
+
| '''Formula'''
−
<FONT SIZE="+1"><math>\Omega_{in} = \Omega - \Omega_s</math></FONT> - the set of interior voxels of an object<br />
+
|-
−
<FONT SIZE="+1"><math>G</math></FONT> - the magnitude of intensity gradient at <math>p</math><br />
+
| Volume
−
<FONT SIZE="+1"><math>\bar{p}</math></FONT> - the center of mass of the object<br />
+
| voxels
−
<FONT SIZE="+1"><math>P</math></FONT> - the normalized histogram of the intensities<br />
+
| Number of voxels in the object [1]
−
<FONT SIZE="+1"><math>P(I)</math></FONT> - normalized histogram of intensity values <math>I</math><br />
+
| <math>|\Omega|</math> or <math>M_{000}|\{I=binary\}</math>
 +
|-
 +
| Integrated Intensity
 +
|
 +
| Sum of the intensities of all voxels in the object [1]
 +
| <math>\sum I(\Omega)</math> or <math>M_{000}|\{I=intensity\}</math>
 +
|-
 +
| Centroid
 +
| voxels
 +
| Center of the object [1]
 +
| <math> \left [ \begin{array}{ccc} \frac{M_{100}}{M_{000}}, & \frac{M_{010}}{M_{000}}, & \frac{M_{001}}{M_{000}} \end{array} \right ]|\{I=binary\} </math>
 +
|-
 +
| Weighted Centroid
 +
| voxels
 +
| Uses the image intensity values to calculate the center of mass of the object [1]
 +
| <math> \left [ \begin{array}{ccc} \frac{M_{100}}{M_{000}}, & \frac{M_{010}}{M_{000}}, & \frac{M_{001}}{M_{000}} \end{array} \right ]|\{I=intensity\} </math>
 +
|-
 +
| Axes Lengths
 +
| voxels
 +
| The length of the axes of the ND hyper-ellipsoid fit to the object [1]
 +
| <math>4\sqrt{\lambda_i}</math>
 +
|-
 +
| Eccentricity
 +
|
 +
| Ratio of the distance between the foci of the best-fit hyper-ellipsoid to the length of its major axis. (2D) [1]
 +
| <math>\sqrt{\frac{\lambda_1 - \lambda_0}{\lambda_1}}</math>
 +
|-
 +
| Elongation
 +
|
 +
| Ratio of the major axis length to minor axis length of the best-fit hyper-ellipsoid. (2D) [1]
 +
| <math>\frac{\lambda_1}{\lambda_0}</math>
 +
|-
 +
| Orientation
 +
| radians
 +
| Angle between the major axis of the best-fit hyper-ellipsoid and origin. (2D) [1]
 +
| <math>tan^{-1}\left(\frac{\overline{v_1}(1)}{\overline{v_1}(0)}\right)</math>
 +
|-
 +
| Bounding Box Volume
 +
| voxels
 +
| Number of voxels in the bounding box of the object [1]
 +
| (max(X)-min(X)+1) * (max(Y)-min(Y)+1) * ...
 +
|-
 +
| Oriented Bounding Box Volume
 +
| voxels
 +
| Number of voxels in the oriented bounding box of the object. The oriented bounding box is defined as the bounding box aligned along the axes of the object. [1]
 +
|
 +
|-
 +
| Sum
 +
|
 +
| Same as integrated intensity [2]
 +
| <math>\sum I(\Omega)</math> or <math>M_{000}|\{I=intensity\}</math>
 +
|-
 +
| Mean
 +
|
 +
| Average intensity of voxels in the object [2]
 +
| <math>\frac{1}{|\Omega|}\sum I(\Omega)</math>
 +
|-
 +
| Median
 +
|
 +
| Middle intensity of voxels in the object [2]
 +
|
 +
|-
 +
| Minimum
 +
|
 +
| Minimum intensity of voxels in the object [2]
 +
|
 +
|-
 +
| Maximum
 +
|
 +
| Maximum intensity of voxels in the object [2]
 +
|
 +
|-
 +
| Sigma
 +
|
 +
| Standard deviation of intensity of voxels in the object [2]
 +
| <math>\sigma_I</math>
 +
|-
 +
| Variance
 +
|
 +
| Variance of intensity of voxels in the object [2]
 +
| <math>\sigma_I^2</math>
 +
|-
 +
| Radius Variation
 +
| voxels
 +
| Standard deviation of distance from surface voxels to centroid
 +
| stddev<math>(\|\Omega_s - \overline{p}\|)</math>
 +
|-
 +
| Skew
 +
|
 +
| Skew of the PDF [3]
 +
| <math>\frac{1}{\sigma_I^3}\sum_{I=0}^{255}(I-\overline{I})^3P(I)</math>
 +
|-
 +
| Energy
 +
|
 +
| Energy of the PDF[3]
 +
| <math>\sum_{I=0}^{255}[P(I)]^2</math>
 +
|-
 +
| Entropy
 +
|
 +
| Entropy of the PDF [3]
 +
| <math>-\sum_{I=0}^{255}P(I)\log_2{P(I)}</math>
 +
|-
 +
| Surface Gradient
 +
|
 +
| Average of surface gradients
 +
| <math>mean(G(\Omega_s))</math>
 +
|-
 +
| Interior Gradient
 +
|
 +
| Average of interior gradients
 +
| <math>mean(G(\Omega_{in}))</math>
 +
|-
 +
| Interior Intensity
 +
|
 +
| Average of interior intensities
 +
| <math>mean(I(\Omega_{in}))</math>  
 +
|-
 +
| Surface Intensity
 +
|
 +
| Average of surface intensities
 +
| <math>mean(I(\Omega_s))</math>
 +
|-
 +
| Intensity Ratio
 +
|
 +
| Ratio of surface intensity to interior intensity
 +
| <math>\frac{mean(I(\Omega_s))}{mean(I(\Omega_{in}))}</math>
 +
|-
 +
| Shared Boundary
 +
|
 +
| Ratio of object "edges" that touch another object to total number of object "edges
 +
|
 +
|-
 +
| Surface Area
 +
| voxels
 +
| Number of voxels on surface of the object [4]
 +
| <math>|\Omega_s|</math>
 +
|-
 +
| Shape
 +
|
 +
| Ratio of surface voxels to total voxels - compactness or thinness of object [5]
 +
| <math>\frac{|\Omega_s|^3}{36\pi|\Omega|^2}</math>
 +
|}
  
−
==External Links==
+
== References ==
−
[http://www.insight-journal.org/browse/publication/301 itkLabelGeometryImageFilter]
+
[1] [http://www.insight-journal.org/browse/publication/301 itkLabelGeometryImageFilter]<br>
−
 
+
[2] [http://www.itk.org/Doxygen312/html/classitk_1_1LabelStatisticsImageFilter.html itkLabelStatisticsImageFilter]<br>
−
[http://kitware.com/products/archive/kitware_quarterly0109.pdf Kitware Source Newsletter]
+
[3] Umbaugh, S. E., Y.-S. Wei, et al. (1997). "Feature extraction in image analysis. A program for facilitating data reduction in medical image classification." Engineering in Medicine and Biology Magazine, IEEE 16(4): 62-73.<br>
 +
[4] Lohmann, G. (1998). Volumetric Image Analysis, Wiley <br>
 +
[5] Theodoridis, S. and K. Koutroumbas (1999). Pattern recognition. San Diego, Academic Press. <br>
 +
[6] [http://kitware.com/products/archive/kitware_quarterly0109.pdf Kitware Source Newsletter]

Latest revision as of 18:39, 27 May 2009

These features can be calculated with two input images (Data Image and Label Image). They are most commonly used for blob-like regions, such as cell nuclei. Equations are shown for 3-dimensional space unless otherwise noted.

Glossary of Notation

p = (x,y,z) the coordinate of a voxel (three-dimensional point in a volume image)
Np a neighbor voxel of p
lp the segmentation label at p
Ii(p) the intensity value of p at ith
Ω = {p | lp = o} the set of voxels of an object o
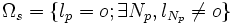
\Omega_s = \{l_p = o; \exists N_p, l_{N_p} \neq o\} the set of surface voxels of the object
Ωin = Ω − Ωs the set of interior voxels of an object
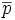
\overline{p} the center of mass of the object
P(I) Probability Density Function (PDF) of intensity values I
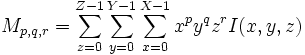
M_{p,q,r} = \sum_{z=0}^{Z-1}\sum_{y=0}^{Y-1}\sum_{x=0}^{X-1}x^p y^q z^r I(x,y,z) Raw Moment of discrete image I
λi ith eigenvalue of covariance matrix
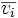
\overline{v_i} eigenvector corresponding to λi

Features

Name Units Description Formula
Volume voxels Number of voxels in the object [1] | Ω | or M000 | {I = binary}
Integrated Intensity Sum of the intensities of all voxels in the object [1] 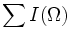\sum I(\Omega) or M000 | {I = intensity}
Centroid voxels Center of the object [1] \left [ \begin{array}{ccc} \frac{M_{100}}{M_{000}}, & \frac{M_{010}}{M_{000}}, & \frac{M_{001}}{M_{000}} \end{array} \right ]|\{I=binary\}
Weighted Centroid voxels Uses the image intensity values to calculate the center of mass of the object [1] \left [ \begin{array}{ccc} \frac{M_{100}}{M_{000}}, & \frac{M_{010}}{M_{000}}, & \frac{M_{001}}{M_{000}} \end{array} \right ]|\{I=intensity\}
Axes Lengths voxels The length of the axes of the ND hyper-ellipsoid fit to the object [1] 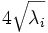4\sqrt{\lambda_i}
Eccentricity Ratio of the distance between the foci of the best-fit hyper-ellipsoid to the length of its major axis. (2D) [1] 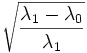\sqrt{\frac{\lambda_1 - \lambda_0}{\lambda_1}}
Elongation Ratio of the major axis length to minor axis length of the best-fit hyper-ellipsoid. (2D) [1] 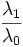\frac{\lambda_1}{\lambda_0}
Orientation radians Angle between the major axis of the best-fit hyper-ellipsoid and origin. (2D) [1] 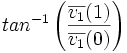tan^{-1}\left(\frac{\overline{v_1}(1)}{\overline{v_1}(0)}\right)
Bounding Box Volume voxels Number of voxels in the bounding box of the object [1] (max(X)-min(X)+1) * (max(Y)-min(Y)+1) * ...
Oriented Bounding Box Volume voxels Number of voxels in the oriented bounding box of the object. The oriented bounding box is defined as the bounding box aligned along the axes of the object. [1]
Sum Same as integrated intensity [2] 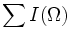\sum I(\Omega) or M000 | {I = intensity}
Mean Average intensity of voxels in the object [2] 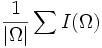\frac{1}{|\Omega|}\sum I(\Omega)
Median Middle intensity of voxels in the object [2]
Minimum Minimum intensity of voxels in the object [2]
Maximum Maximum intensity of voxels in the object [2]
Sigma Standard deviation of intensity of voxels in the object [2] σI
Variance Variance of intensity of voxels in the object [2] 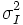\sigma_I^2
Radius Variation voxels Standard deviation of distance from surface voxels to centroid stddev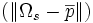(\|\Omega_s - \overline{p}\|)
Skew Skew of the PDF [3] 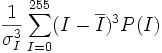\frac{1}{\sigma_I^3}\sum_{I=0}^{255}(I-\overline{I})^3P(I)
Energy Energy of the PDF[3] \sum_{I=0}^{255}[P(I)]^2
Entropy Entropy of the PDF [3] 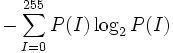-\sum_{I=0}^{255}P(I)\log_2{P(I)}
Surface Gradient Average of surface gradients mean(G(Ωs))
Interior Gradient Average of interior gradients mean(G(Ωin))
Interior Intensity Average of interior intensities mean(I(Ωin))
Surface Intensity Average of surface intensities mean(I(Ωs))
Intensity Ratio Ratio of surface intensity to interior intensity 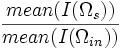\frac{mean(I(\Omega_s))}{mean(I(\Omega_{in}))}
Shared Boundary Ratio of object "edges" that touch another object to total number of object "edges
Surface Area voxels Number of voxels on surface of the object [4] | Ωs |
Shape Ratio of surface voxels to total voxels - compactness or thinness of object [5] 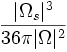\frac{|\Omega_s|^3}{36\pi|\Omega|^2}

References

[1] itkLabelGeometryImageFilter
[2] itkLabelStatisticsImageFilter
[3] Umbaugh, S. E., Y.-S. Wei, et al. (1997). "Feature extraction in image analysis. A program for facilitating data reduction in medical image classification." Engineering in Medicine and Biology Magazine, IEEE 16(4): 62-73.
[4] Lohmann, G. (1998). Volumetric Image Analysis, Wiley
[5] Theodoridis, S. and K. Koutroumbas (1999). Pattern recognition. San Diego, Academic Press.
[6] Kitware Source Newsletter

Retrieved from "http://farsight-toolkit.ee.uh.edu/wiki/Intrinsic_Features_of_Blobs"
Personal tools