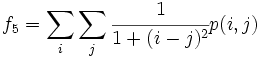Equations for 3D Haralick Texture Feature

From FarsightWiki
(Difference between revisions)
Jump to: navigation, search
(→Notation)
(→Notation)
Line 12: Line 12:
  
 
      
 
      
−
   --<math>p_{x+y}(k):</math> <math> p_{x+y}(k) = \sum_{i=0}^{N_g} \sum_{j=0,i+j=k}^{N_g} p(i,j), k=2,3,...,2N_g </math>
+
   --<math>p_{x+y}(k):</math> <math> p_{x+y}(k) = \sum_{i=1}^{N_g} \sum_{j=1,i+j=k}^{N_g} p(i,j), k=2,3,...,2N_g </math>
  
−
   --<math>p_{x-y}(k):</math> <math> p_{x-y}(k) = \sum_{i=0}^{N_g} \sum_{j=0,|i-j|=k}^{N_g} p(i,j), k=0,1,...,N_g-1 </math>
+
   --<math>p_{x-y}(k):</math> <math> p_{x-y}(k) = \sum_{i=1}^{N_g} \sum_{j=1,|i-j|=k}^{N_g} p(i,j), k=0,1,...,N_g-1 </math>
 +
 
 +
==Textural Features==
 +
* 1) Angular Second Moment:<math>f_1 =  \sum_{i=1}^{N_g}  \sum_{j=1}^{N_g} p(i,j)^2 </math>
 +
* 2) Contrast:<math>f_2 =  \sum_{n=0}^{N_g - 1} n^2 {\sum_{i=1}^{N_g} \sum_{j=1,|i-j|=n}^{N_g} p(i,j)} </math>
 +
* 3) Correlation:<math>f_3 = \cfrac{\sum_i \sum_j (i,j)p(i,j)-u_x u_y}{\sigma_x \sigma_y}</math>
 +
* 4) Sum of the Squares of Variance: <math>f_4 = \sum_{i=1}^{N_g} \sum_{j=1}^{N_g} (i-j)^2 p(i,j)</math>
 +
* 5) Inverse Difference Moment: <math>f_5 = \sum_i \sum_j \cfrac{1}{1+(i-j)^2}p(i,j)</math>

Revision as of 02:47, 27 April 2009

Notation

  --p(i,j): (i,j)th entry in a normalized gray-tone spatial dependence matrix, p(i,j) = P(i,j) / R
    * P(i,j) is the co-occurrence matrix and R is the sum of values in it, thus P(i,j) can be  considered as the joint distribution 
    of i and j, which are gray levels of the original image. The value of entry p(i,j) is supposed to be very small due to the 
    large size of the co-occurrence matrix.

  --px(i) / py(i): ith entry in the marginal-probability distribution matrix obtained by summing the rows/columns of p(i,j).

  --Ng: Number of distinct gray levels in the image.



  --px + y(k):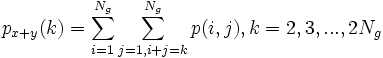  p_{x+y}(k)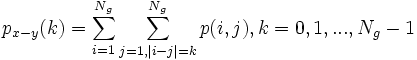 = \sum_{i=1}^{N_g} \sum_{j=1,i+j=k}^{N_g} p(i,j), k=2,3,...,2N_g 

  --px − y(k):  p_{x-y}(k) = \sum_{i=1}^{N_g} \sum_{j=1,|i-j|=k}^{N_g} p(i,j), k=0,1,...,N_g-1

Textural Features

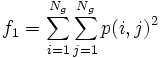
  • 1) Angular Second Moment:f_1 = \sum_{i=1}^{N_g} \sum_{j=1}^{N_g} p(i,j)^2
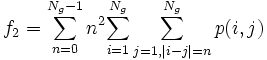
  • 2) Contrast:f_2 = \sum_{n=0}^{N_g - 1} n^2 {\sum_{i=1}^{N_g} \sum_{j=1,|i-j|=n}^{N_g} p(i,j)}
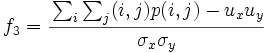
  • 3) Correlation:f_3 = \cfrac{\sum_i \sum_j (i,j)p(i,j)-u_x u_y}{\sigma_x \sigma_y}
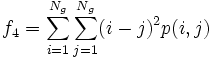
  • 4) Sum of the Squares of Variance: f_4 = \sum_{i=1}^{N_g} \sum_{j=1}^{N_g} (i-j)^2 p(i,j)
  • 5) Inverse Difference Moment: f_5 = \sum_i \sum_j \cfrac{1}{1+(i-j)^2}p(i,j)
Retrieved from "http://farsight-toolkit.ee.uh.edu/wiki/Equations_for_3D_Haralick_Texture_Feature"
Personal tools