Equations for 3D Haralick Texture Feature

From FarsightWiki
(Difference between revisions)
Jump to: navigation, search
(→Notation)
 
(One intermediate revision by one user not shown)
Line 1: Line 1:
 +
Equations for 3D Haralick Texture features[1], which are based in a gray-level co-occurrence matrix of the image
 
==Notation==
 
==Notation==
 
   
 
   
Line 17: Line 18:
 
   --<math>p_{x-y}(k):</math> <math> p_{x-y}(k) = \sum_{i=1}^{N_g} \sum_{j=1,|i-j|=k}^{N_g} p(i,j), k=0,1,...,N_g-1 </math>
 
   --<math>p_{x-y}(k):</math> <math> p_{x-y}(k) = \sum_{i=1}^{N_g} \sum_{j=1,|i-j|=k}^{N_g} p(i,j), k=0,1,...,N_g-1 </math>
  
−
For more information about the Textural features, please refer to [1].
 
−
== Reference ==
 
−
* [1] R. Haralick, K. Shanmugam, and I. Dinstein, "Textural features for image classification," IEEE Transactions on Systems, Man, and Cybernetics, SMC-3, 610-621, 1973.
 
  
 
==Textural Features==
 
==Textural Features==
Line 37: Line 35:
 
<math>HXY1 = -\sum_{i=1}^{N_g} \sum_{j=1}^{N_g} p(i,j)log(p_x(i) p_y(i))</math>,
 
<math>HXY1 = -\sum_{i=1}^{N_g} \sum_{j=1}^{N_g} p(i,j)log(p_x(i) p_y(i))</math>,
 
<math>HXY2 = -\sum_{i=1}^{N_g} \sum_{j=1}^{N_g} p_x(i)p_y(j)log(p_x(i) p_y(i))</math>
 
<math>HXY2 = -\sum_{i=1}^{N_g} \sum_{j=1}^{N_g} p_x(i)p_y(j)log(p_x(i) p_y(i))</math>
 +
 +
For more information about the Textural features, please refer to [1].
 +
== Reference ==
 +
* [1] R. Haralick, K. Shanmugam, and I. Dinstein, "Textural features for image classification," IEEE Transactions on Systems, Man, and Cybernetics, SMC-3, 610-621, 1973.

Latest revision as of 03:22, 27 April 2009

Equations for 3D Haralick Texture features[1], which are based in a gray-level co-occurrence matrix of the image

Notation

  --p(i,j): (i,j)th entry in a normalized gray-tone spatial dependence matrix, p(i,j) = P(i,j) / R
    * P(i,j) is the co-occurrence matrix and R is the sum of values in it, thus P(i,j) can be  considered as the joint distribution 
    of i and j, which are gray levels of the original image. The value of entry p(i,j) is supposed to be very small due to the 
    large size of the co-occurrence matrix.

  --px(i) / py(i): ith entry in the marginal-probability distribution matrix obtained by summing the rows/columns of p(i,j).

  --Ng: Number of distinct gray levels in the image.



  --px + y(k):  p_{x+y}(k) = \sum_{i=1}^{N_g} \sum_{j=1,i+j=k}^{N_g} p(i,j), k=2,3,...,2N_g 
    px + y(i) is the probability of co-occurrence matrix coordinates summing to x+y

  --px − y(k):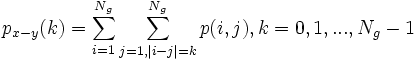  p_{x-y}(k) = \sum_{i=1}^{N_g} \sum_{j=1,|i-j|=k}^{N_g} p(i,j), k=0,1,...,N_g-1


Textural Features

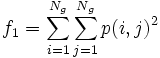
  • 1) Angular Second Moment:f_1 = \sum_{i=1}^{N_g} \sum_{j=1}^{N_g} p(i,j)^2
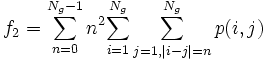
  • 2) Contrast:f_2 = \sum_{n=0}^{N_g - 1} n^2 {\sum_{i=1}^{N_g} \sum_{j=1,|i-j|=n}^{N_g} p(i,j)}
  • 3) Correlation: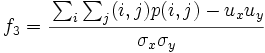f_3 = \cfrac{\sum_i \sum_j (i,j)p(i,j)-u_x u_y}{\sigma_x \sigma_y}, where ux,uy,σx,σy are the means and std.deviations of px and py, the partial probability density functions
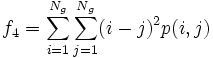
  • 4) Sum of the Squares of Variance: f_4 = \sum_{i=1}^{N_g} \sum_{j=1}^{N_g} (i-j)^2 p(i,j)
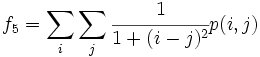
  • 5) Inverse Difference Moment: f_5 = \sum_i \sum_j \cfrac{1}{1+(i-j)^2}p(i,j)
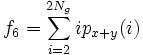
  • 6) Sum Average: f_6 = \sum_{i=2}^{2N_g} ip_{x+y}(i)
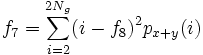
  • 7) Sum Variance: f_7 = \sum_{i=2}^{2N_g}(i-f_8)^2 p_{x+y}(i)
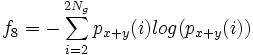
  • 8) Sum Entropy: f_8 = - \sum_{i=2}^{2N_g}p_{x+y}(i)log(p_{x+y}(i))
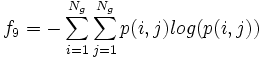
  • 9) Entropy: f_9 = -\sum_{i=1}^{N_g} \sum_{j=1}^{N_g} p(i,j)log(p(i,j))
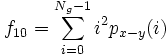
  • 10) Difference Variance: f_{10} = \sum_{i=0}^{N_g-1} i^2 p_{x-y}(i)
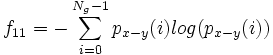
  • 11) Difference Entropy: f_{11}= -\sum_{i=0}^{N_g-1} p_{x-y}(i)log(p_{x-y}(i))
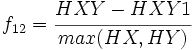
  • 12) Information Measures of Correlation 1: f_{12} = \cfrac{HXY-HXY1}{max(HX,HY)}
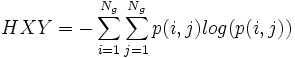  • 13) Information Measures of Correlation 2: f13 = (1 − exp( − 2.0 | HXY2 − HXY | ))1 / 2, with HXY = -\sum_{i=1}^{N_g} \sum_{j=1}^{N_g} p(i,j)log(p(i,j)),

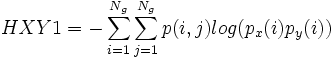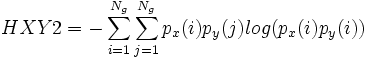
HXY1 = -\sum_{i=1}^{N_g} \sum_{j=1}^{N_g} p(i,j)log(p_x(i) p_y(i)), HXY2 = -\sum_{i=1}^{N_g} \sum_{j=1}^{N_g} p_x(i)p_y(j)log(p_x(i) p_y(i))

For more information about the Textural features, please refer to [1].

Reference

  • [1] R. Haralick, K. Shanmugam, and I. Dinstein, "Textural features for image classification," IEEE Transactions on Systems, Man, and Cybernetics, SMC-3, 610-621, 1973.
Retrieved from "http://farsight-toolkit.ee.uh.edu/wiki/Equations_for_3D_Haralick_Texture_Feature"
Personal tools