Intrinsic Features of Blobs

From FarsightWiki
(Difference between revisions)
Jump to: navigation, search
(→Glossary of Notation)
Line 31: Line 31:
 
|-
 
|-
 
| <math>P(I)</math>
 
| <math>P(I)</math>
−
| normalized histogram of intensity values <math>I</math>
+
| Probability Density Function (PDF) of intensity values <math>I</math>
 
|-
 
|-
 
| <math>M_{p,q,r} = \sum_{z=0}^{Z-1}\sum_{y=0}^{Y-1}\sum_{x=0}^{X-1}x^p y^q z^r I(x,y,z)</math>
 
| <math>M_{p,q,r} = \sum_{z=0}^{Z-1}\sum_{y=0}^{Y-1}\sum_{x=0}^{X-1}x^p y^q z^r I(x,y,z)</math>

Revision as of 18:28, 27 May 2009

These features can be calculated with two input images (Data Image and Label Image). They are most commonly used for blob-like regions, such as cell nuclei. Equations are shown for 3-dimensional space unless otherwise noted.

Glossary of Notation

p = (x,y,z) the coordinate of a voxel (three-dimensional point in a volume image)
Np a neighbor voxel of p
lp the segmentation label at p
Ii(p) the intensity value of p at ith
Ω = {p | lp = o} the set of voxels of an object o
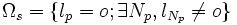
\Omega_s = \{l_p = o; \exists N_p, l_{N_p} \neq o\} the set of surface voxels of the object
Ωin = Ω − Ωs the set of interior voxels of an object
\bar{p} the center of mass of the object
P(I) Probability Density Function (PDF) of intensity values I
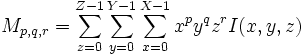
M_{p,q,r} = \sum_{z=0}^{Z-1}\sum_{y=0}^{Y-1}\sum_{x=0}^{X-1}x^p y^q z^r I(x,y,z) Raw Moment of discrete image I
λi ith eigenvalue of covariance matrix
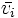
\bar{v_i} eigenvector corresponding to λi

Features

Name Units Description Formula
Volume voxels Number of voxels in the object [1] | Ω | or M000 | {I = binary}
Integrated Intensity Sum of the intensities of all voxels in the object [1] 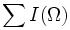\sum I(\Omega) or M000 | {I = intensity}
Centroid voxels Center of the object [1] \left [ \begin{array}{ccc} \frac{M_{100}}{M_{000}}, & \frac{M_{010}}{M_{000}}, & \frac{M_{001}}{M_{000}} \end{array} \right ]|\{I=binary\}
Weighted Centroid voxels Uses the image intensity values to calculate the center of mass of the object [1] \left [ \begin{array}{ccc} \frac{M_{100}}{M_{000}}, & \frac{M_{010}}{M_{000}}, & \frac{M_{001}}{M_{000}} \end{array} \right ]|\{I=intensity\}
Axes Lengths voxels The length of the axes of the ND hyper-ellipsoid fit to the object [1] 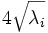4\sqrt{\lambda_i}
Eccentricity Ratio of the distance between the foci of the best-fit hyper-ellipsoid to the length of its major axis. (2D) [1] \sqrt{\frac{\lambda_1 - \lambda_0}{\lambda_1}}
Elongation Ratio of the major axis length to minor axis length of the best-fit hyper-ellipsoid. (2D) [1] 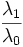\frac{\lambda_1}{\lambda_0}
Orientation radians Angle between the major axis of the best-fit hyper-ellipsoid and origin. (2D) [1] tan^{-1}(\frac{\bar{v_1}(1)}{\bar{v_1}(0)})
Bounding Box Volume voxels Number of voxels in the bounding box of the object [1] (max(X)-min(X)+1) * (max(Y)-min(Y)+1) * ...
Oriented Bounding Box Volume voxels Number of voxels in the oriented bounding box of the object. The oriented bounding box is defined as the bounding box aligned along the axes of the object. [1]
Sum Same as integrated intensity [2] 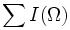\sum I(\Omega) or M000 | {I = intensity}
Mean Average intensity of voxels in the object [2] 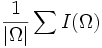\frac{1}{|\Omega|}\sum I(\Omega)
Median Middle intensity of voxels in the object [2]
Minimum Minimum intensity of voxels in the object [2]
Maximum Maximum intensity of voxels in the object [2]
Sigma Standard deviation of intensity of voxels in the object [2] σI
Variance Variance of intensity of voxels in the object [2] 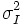\sigma_I^2
Radius Variation voxels Standard deviation of distance from surface voxels to centroid stddev(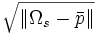\sqrt{\|\Omega_s - \bar{p}\|}
Skew Skew of the normalized intensity histogram [3] \frac{1}{\sigma_I^3}\sum_{I=0}^{255}(I-\bar{I})^3P(I)
Energy Energy of the normalized intensity histogram [3] \sum_{I=0}^{255}[P(I)]^2
Entropy Entropy of the normalized intensity histogram [3] -\sum_{I=0}^{255}P(I)\log_2{P(I)}
Surface Gradient Average of surface gradients mean(G(Ωs))
Interior Gradient Average of interior gradients mean(G(Ωin))
Interior Intensity Average of interior intensities mean(I(Ωin))
Surface Intensity Average of surface intensities mean(I(Ωs))
Intensity Ratio Ratio of surface intensity to interior intensity 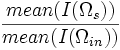\frac{mean(I(\Omega_s))}{mean(I(\Omega_{in}))}
Shared Boundary Ratio of object "edges" that touch another object to total number of object "edges
Surface Area voxels Number of voxels on surface of the object [4] | Ωs |
Shape Ratio of surface voxels to total voxels - compactness or thinness of object [5] 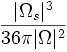\frac{|\Omega_s|^3}{36\pi|\Omega|^2}


References

[1] itkLabelGeometryImageFilter
[2] itkLabelStatisticsImageFilter
[3] Umbaugh, S. E., Y.-S. Wei, et al. (1997). "Feature extraction in image analysis. A program for facilitating data reduction in medical image classification." Engineering in Medicine and Biology Magazine, IEEE 16(4): 62-73.
[4] Lohmann, G. (1998). Volumetric Image Analysis, Wiley
[5] Theodoridis, S. and K. Koutroumbas (1999). Pattern recognition. San Diego, Academic Press.
[6] Kitware Source Newsletter

Retrieved from "http://farsight-toolkit.ee.uh.edu/wiki/Intrinsic_Features_of_Blobs"
Personal tools