Features
| Line 43: | Line 43: | ||
'''2. Associative Features: ''' Associative features quantify associations/relationships between objects. They can be computed once objects have been delineated, and assigned unique identifiers (IDs). | '''2. Associative Features: ''' Associative features quantify associations/relationships between objects. They can be computed once objects have been delineated, and assigned unique identifiers (IDs). | ||
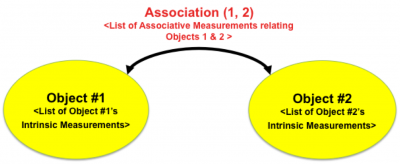
| − | [[Image:Association.png | center| | + | [[Image:Association.png | center| 400px| Illustrating the notion of an associative measurement linking two objects. The list of associative measurements is dependent upon the nature of the two objects and the nature of the relationship between them that we are interested in quantifying. Graph theory offers a natural mathematical representation for associations.]] |
Some associative features involve objects and image data. Others relate objects to other objects. Associative features are quite diverse, and there are a combinatorially large number of possible associations. However, a much smaller number of them are are interesting and/or useful for a given investigation. The goal of FARSIGHT is to have a versatile set of 'programmable' computational methods available to the user. These are based on the simplest notions such as spatial proximity, neighborhood, and adjacency. | Some associative features involve objects and image data. Others relate objects to other objects. Associative features are quite diverse, and there are a combinatorially large number of possible associations. However, a much smaller number of them are are interesting and/or useful for a given investigation. The goal of FARSIGHT is to have a versatile set of 'programmable' computational methods available to the user. These are based on the simplest notions such as spatial proximity, neighborhood, and adjacency. | ||
Revision as of 13:01, 28 April 2009
FARSIGHT contains a rich and constantly growing library of software routines to compute diverse measurements from images. Measurements are also commonly referred to as "features" in the image analysis community. Broadly speaking, there are two classes of features in FARSIGHT:
1. Intrinsic Features: Intrinsic features are measurements that quantify aspects of the morphology and/or appearance of objects in a single image channel. They can be computed based on a segmentation (object delineation) that results in a set of pixel/voxel labels. One must pay close attention to the units of the features. Also keep in mind the possibility of non-isotropic images - this is a common occurrence in biological microscopy. Usually, the axial dimension of a voxel is much greater than its lateral dimensions. To obtain feature measurements in physical units, one must scale pixel/voxel based feature values appropriately. The intrinsic measurements of each object are directly determined by its morphological class. Some examples are noted in the table below.
| Object Morphology | Examples of Intrinsic Measurements | Link |
|---|---|---|
| Blobs | location, diameter, volume, shape factor, surface area, eccentricity, texture | Intrinsic Features of Blobs |
| Tubes | centerline, surface locations, local diameter, branch/crossover points, orientation | |
| Shells | thickness, shape factors, brightness | |
| Plate/Laminae | thickness, surface area, brightness | |
| Man-made objects | location, pose | |
| Foci | location, brightness, diameter | |
| Cloud | Brightness, texture |
The goal of FARSIGHT is to have a sufficiently rich, and well-documented library of intrinsic features available to the user for each morphological category. Another goal is to incorporate appropriate corrections when possible. For instance, most intensity/brightness measurements require a background correction step. Careful documentation of each feature, and clarifying its properties such as the units and invariance are an important goal.
2. Associative Features: Associative features quantify associations/relationships between objects. They can be computed once objects have been delineated, and assigned unique identifiers (IDs).
Some associative features involve objects and image data. Others relate objects to other objects. Associative features are quite diverse, and there are a combinatorially large number of possible associations. However, a much smaller number of them are are interesting and/or useful for a given investigation. The goal of FARSIGHT is to have a versatile set of 'programmable' computational methods available to the user. These are based on the simplest notions such as spatial proximity, neighborhood, and adjacency.