Object level association
(→Overview) |
|||
| Line 2: | Line 2: | ||
| − | ==Overview== | + | == Overview == |
We present a simple, yet general framework for object-level association between biological objects and/or elements present in the different channels of multi-channel images. The proposed object-level association framework assumes that any association rule is defined between two elements. The first one, which we call the reference element, is the segmented object (such as cells/nuclei) for which we want to quantify some associative relationships. The second element, which we call the target element, is a biologically meaningful element in a different channel. The target element does not have to be segmented or undergone under any kind of processing. | We present a simple, yet general framework for object-level association between biological objects and/or elements present in the different channels of multi-channel images. The proposed object-level association framework assumes that any association rule is defined between two elements. The first one, which we call the reference element, is the segmented object (such as cells/nuclei) for which we want to quantify some associative relationships. The second element, which we call the target element, is a biologically meaningful element in a different channel. The target element does not have to be segmented or undergone under any kind of processing. | ||
| Line 21: | Line 21: | ||
Based on this distance function, the region of interest (RIO) is defined as a region with specific inside and outside (respectively negative and positive) distances. | Based on this distance function, the region of interest (RIO) is defined as a region with specific inside and outside (respectively negative and positive) distances. | ||
| − | ==Running The Program== | + | == Running The Program == |
to be added | to be added | ||
| − | ==Sample Output== | + | == Sample Output == |
to be added | to be added | ||
Revision as of 04:11, 3 May 2009
In this page we give an overview of the distance map-based approach for defining object-level associations
Overview
We present a simple, yet general framework for object-level association between biological objects and/or elements present in the different channels of multi-channel images. The proposed object-level association framework assumes that any association rule is defined between two elements. The first one, which we call the reference element, is the segmented object (such as cells/nuclei) for which we want to quantify some associative relationships. The second element, which we call the target element, is a biologically meaningful element in a different channel. The target element does not have to be segmented or undergone under any kind of processing.
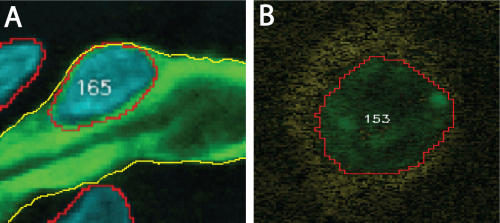
Two association examples are shown in Figure 1 below. In both examples, the reference element is a segmented cell nucleus. However, the target element in the first example (panel A) is a segmented blood vessel. Hence, association occurs between two segmented objects. In the second example (panel B), the target element is a molecular signal (yellow) that may surround some cell nuclei and available in a different channel.
An association rule is composed of two components. The first one defines the region of interest (ROI) associated with the reference elements and on which the associative measure is applied. The second component is an associative measure, which is a mathematical function defined on the regions of interest (ROI) of the reference elements, and used to quantify the associative relationship.
In this work, the region of interest (ROI) corresponding to an association rule is defined using a distance function. Starting from the edge points (segmentation boundary) 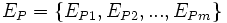 of the reference element E, the distance function DE(x,y) computes the shortest signed Euclidean distance from a point (or in 3-D images) to the boundary points of the reference element:
of the reference element E, the distance function DE(x,y) computes the shortest signed Euclidean distance from a point (or in 3-D images) to the boundary points of the reference element:
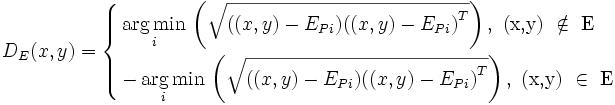 where i = 1,2,...,m
where i = 1,2,...,m
Based on this distance function, the region of interest (RIO) is defined as a region with specific inside and outside (respectively negative and positive) distances.
Running The Program
to be added
Sample Output
to be added