Trace Editor/Features
From FarsightWiki
(Difference between revisions)
m (→Algorithms) |
DavidCerna (Talk | contribs) (→Algorithms) |
||
| Line 32: | Line 32: | ||
*Minimal distance between end points | *Minimal distance between end points | ||
| − | **Angle between traces | + | **[[Angle between traces-]] Consider the direction vector for two endpoint e<sub>1</sub>, e<sub>2</sub> in proximity( this is given by a constant); the direction vectors are d<sub>1</sub> and d<sub>2</sub> respectfully. Using this information we can find the angular change by projecting d<sub>1</sub> onto d<sub>2</sub>, the angular change can be found using the error vector and the direction vectors. We can also draw a triangle using the line connecting e<sub>1</sub> and e<sub>2</sub>, the lines through d<sub>1</sub> and d<sub>2</sub>, and the midpoint line. The second method as of now requires the picture to be projected to 2 dimensions, but this should be easy to extend. |
**Path length | **Path length | ||
**Gap distance is too large | **Gap distance is too large | ||
Revision as of 04:25, 29 June 2009
Feature computation for Trace Editor
Feature List
| Feature | Description |
|---|---|
| Gap Size | Minimum distance between endpoints of two traces |
| Angle | Is the angle created between two traces normalized as vectors |
| Path Length | Total length along a trace, indicated by the size of the trace |
| Euclidean Distance | Straight line distance between the endpoints of a trace |
| Fragmentation Smoothness | Ratio of Path Length to Euclidean Distance[1] |
Algorithms
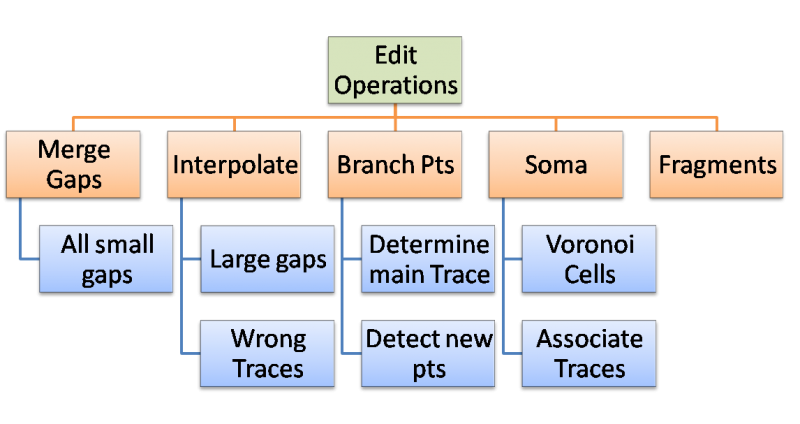
The algorithms suggested are used to control the editing process allowing for rule based cluster editing. The Goal is to complete group editing in five steps.
1: Merge Small Gaps Goal: Create longest continuous trace segments by merging close endpoints Methods: Nearest neighbors (Closest end points),
Rejection based on conflicts and thresholds
- Minimal distance between end points
- Angle between traces- Consider the direction vector for two endpoint e1, e2 in proximity( this is given by a constant); the direction vectors are d1 and d2 respectfully. Using this information we can find the angular change by projecting d1 onto d2, the angular change can be found using the error vector and the direction vectors. We can also draw a triangle using the line connecting e1 and e2, the lines through d1 and d2, and the midpoint line. The second method as of now requires the picture to be projected to 2 dimensions, but this should be easy to extend.
- Path length
- Gap distance is too large
- Another trace is a better fit (Cost Function)
- Smallest gap
- Better Angular alignment
- "Bad merge"
- The merge causes corners
- Needs to be smoothed
2: Interpolate Large Gaps Goal: Connect Large gaps that step 1 cannot simply connect by addition of a single cell Method: Larger gaps need new segments created,
new Trace Bits must be added,
smoothing operator.

Example showing how Merging and branching are interconnected. The Merging that creates sharp turns needs to be smoothed. The Traces need to create a new branch point and trace bits to interpolate the original *Curve fitting to find trend of: **Direction **Curvature *Interpolation **Extend the line **Most probable vector **Avoid creating edges path of the branch.
3: Branch Points Goal: Detect and control Branching Method: Detect most probable intercepts,
Determination of main branch and child,
Type of branch point
- Distance maps
- Nearest neighbors (traces)
- Closest trace bits
- Angle of intercept
- Interpolation
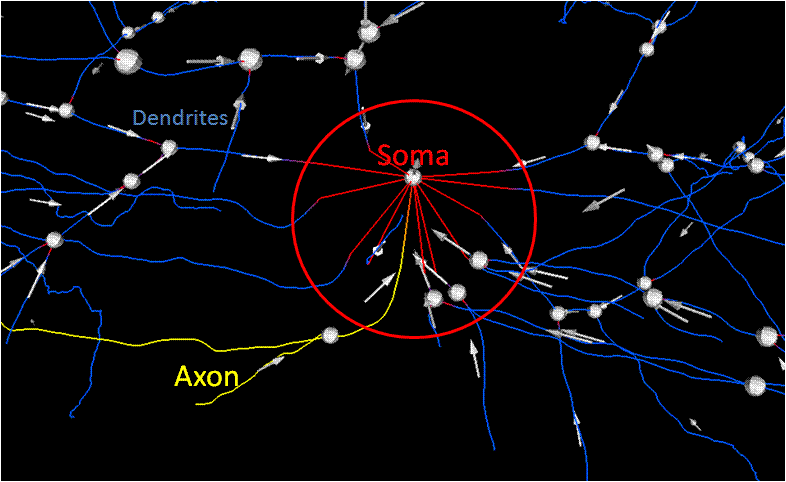
4: Soma Detection Goal: Correspond processes with a soma Method: Segmentation of original data,
Localize the area to attach processes to soma,
Correct direction of traces
- Image intensity
- Blob segmentation
- Centroid
- Distance map
- Connectivity
- Connected components
- Localization of processes
5: Fragments Goal: Removal of small traces that do not correspond to a process Method: Small traces removed,
Leftovers from splitting operators,
Line fragments that cannot be merged
- Lowest percentile of length
- Traces with no parents or children
- Type dependent
Cite error:
<ref> tags exist, but no <references/> tag was found