Trace Editor/Features
(→Definition of the Trace Structure and associated objects) |
(→Trace Structure) |
||
| Line 1: | Line 1: | ||
= '''Trace Structure''' = | = '''Trace Structure''' = | ||
| − | To handle all of the traces the editor uses a tree structure. Neuron branching can be represented as series of points with parents and children. The Inputs Traces to the trace editor can be either | + | To handle all of the traces the editor uses a tree structure. Neuron branching can be represented as series of points with parents and children. The Inputs Traces to the trace editor can be either SWC, or RPIXML format. |
| + | The RPIXML format can be extended to read in extra computed features, that may be specific to a data type or algorithm, by including a header with the features to search for. | ||
<pre> | <pre> | ||
Revision as of 20:57, 3 September 2009
Contents |
Trace Structure
To handle all of the traces the editor uses a tree structure. Neuron branching can be represented as series of points with parents and children. The Inputs Traces to the trace editor can be either SWC, or RPIXML format. The RPIXML format can be extended to read in extra computed features, that may be specific to a data type or algorithm, by including a header with the features to search for.
<FeatureHeaderNames> HeadSize,SpineLength,SpineSize,HeadToLengthRatio,DistanceToDendrite,Intensity </FeatureHeaderNames>
Defining the Features to compute in the XML file. The XML file reader will find all traces with associated features which will show in the linked space views.
<TraceLine ID="1" Type="1" Parent="-1"> <TraceBit ID="1" X="0.81" Y="255.81" Z="50.55"/> </TraceLine> <!--Dendrite ID=1-->
TraceLine 1 is a dendrite (type 1), consisting of 1 trace bit, and has no parent (indicated by the -1). There are no extra features calculated for this trace.
<TraceLine ID="2" Type="5" Parent="1" HeadSize="0.000" SpineLength="7.828" SpineSize="14.000" HeadToLengthRatio="0.000" DistanceToDendrite="1.178" Intensity="146.856"> <TraceBit ID="1" X="4.00" Y="255.00" Z="50.00"/> <TraceBit ID="5" X="3.00" Y="254.00" Z="49.00"/> <TraceBit ID="9" X="2.00" Y="254.00" Z="49.00"/> <TraceBit ID="13" X="2.00" Y="253.00" Z="48.00"/> <TraceBit ID="17" X="2.00" Y="253.00" Z="47.00"/> <TraceBit ID="21" X="2.00" Y="253.00" Z="47.00"/> </TraceLine> <!--Ending Spine ID=2-->
TraceLine 2 is a spine (type 5), consisting of 6 trace bits, and has a parent TraceLine 1. There are 6 extra features computed and are defined in the Feature Header Names.
Trace Bit
The Trace Bit is the basic unit of the trace structure as a point in 3d space (x,y,z).
Each bit also stores the radius and an ID.
Trace Line
Trace Lines are lists of trace bits maintaining the order of connectivity.
Each Trace Line has a unique ID.
Each stores a pointer to any parents or children(branches).
Trace Lines have a type (soma, dendrite...) that defines its properties.
Trace Object
The Trace Object is a container of all the traces.
This is responsible for creating the VTK structure, functions modifying the tree structure, and handling file input/output.
Trace Gap
A trace gap is an object representing an associative measurement between the smallest separation of the endpoints of two trace Lines.
This is used in merging to recconect fragmented traces.
Features and algorithms for Trace Editor
The Trace Editor uses several intrinsic and computed features in both manual and automated processes.
Most features used for editing operate on the trace lines or the gaps.
For specific neural structures such as dendritic spines further features may be computed.
Feature List
| Feature | Description | Equation or Variable |
|---|---|---|
| Gap Size | Minimum distance between endpoints of two traces | 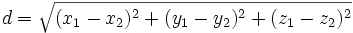
|
| Angle | The angle created between two traces normalized as vectors | 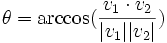
|
| Path Length | Total length along a trace, indicated by the size of the trace | 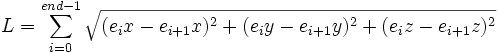
|
| Euclidean Distance | Straight line distance between the endpoints of a trace | 
|
| Fragmentation Smoothness | Ratio of Path Length to Euclidean Distance [1] | 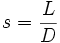
|
| Maximum Gap Distance | The maximum distance between endpoints that can be merged | Δ |
| Weights | The weights are used in the cost1 algorithm | α β |
| Cost1 | Weighted scalar evaluating the merge [2] | 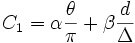
|
| Cost2 | Weighted scalar with Fragmentation Smoothness | ![C_2=\theta[\frac{d}{\Delta}]s](/mw/images/math/8/3/8/838dc6bcf55d56903864da4855c33cca.png)
|
| Curvature | The Hessian matrix for checking branching point existence and interpolating the path. (Still under consideration) | ![\left[\begin{array}{ccc}
f(x)_{xx}(X) + \frac{\alpha}{2}f_{yy}(X) + \frac{\alpha}{2}f_{zz}(X) & (1-\alpha)f_{xy}(X) & (1-\alpha)f_{xz}(X) \\
(1-\alpha)f_{xy}(X) & f_{yy}(X) + \frac{\alpha}{2}f(x)_{xx}(X) +\frac{\alpha}{2}f_{zz}(X) & (1-\alpha)f_{yz}(X) \\
(1-\alpha)f_{xz}(X) & (1-\alpha)f_{yz}(X) & f_{zz}(X) + \frac{\alpha}{2}f(x)_{xx}(X) +\frac{\alpha}{2}f_{yy}(X)
\end{array} \right]](/mw/images/math/8/6/2/86265c277f698370dbb9b8bbf95c9619.png)
|
| Parent | Considering that neurites branching out from the soma form a tree-like structure, a parent point can be used to find a cycle. | |
| Tortuosity | Seee section on Tortuosity. Will be up shortly. Considering dividing the arccos() and the polygon angle sum by Pi for neatness and simplicity reasons. | 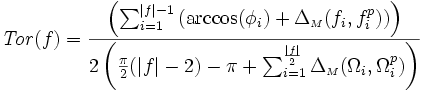
2) 3) For 4) φi is based on the law of cosines, it is 5) 6) M is the midpoint of the line between f0 and f | f | . 7) 8) 9) 10) M' is the midpoint of the line between f0 and M. 11) 12) |
Algorithms
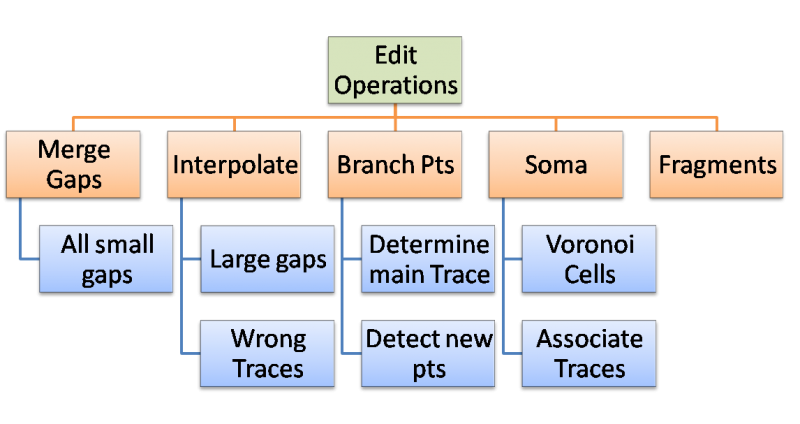
The algorithms suggested are used to control the editing process allowing for rule based cluster editing. The Goal is to complete group editing in five steps.
Merge Small Gaps
Goal: Create longest continuous trace segments by merging close endpoints Methods: Nearest neighbors (Closest end points),
Rejection based on conflicts and thresholds
- Minimal distance between end points
- Angle between traces- The angle is measured between the two traces by computing the norm of their vectors and the dot product.
The equation is: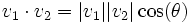 which when solved for θ is:
which when solved for θ is: 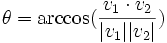
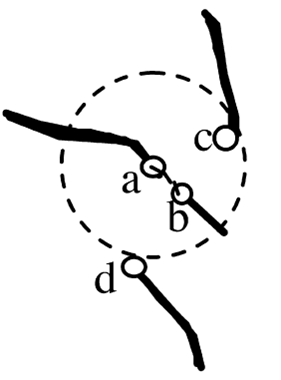
- Path length- The path length is considered if the end points are not the best fit for the merge. For instance, a merging that would cause a sharp peak in the neurite. This is a more serious problem for large gaps (see below). To help alleviate this for small gaps, merge at the point where the direction changes sharply.
- Gap distance is too large- The distance between the two points e_1, e_2 is computed to save computation. If the distance is longer than the excepted small gap distance, then the traces will not be considered for merging. A cost function adapted from "Automated Three-Dimensional Tracing of Neurons in Confocal and Brightfield Images" will take into account small gaps with two end points.
- Consider possibility of loops Though less probable in 3D, often there are 2D projections of 3D images resulting in loops being in the images. Loops in the branching structure can be avoided by checking the parents, as a trace cannot have two parents, but there can be two children.
- Angle between traces- The angle is measured between the two traces by computing the norm of their vectors and the dot product.
- Another trace is a better fit (Cost Function)
- Smallest gap
- Better Angular alignment
- "Bad merge"
- The merge causes corners
- Needs to be smoothed
The Cost function we have implemented is modified from:
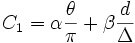
to include fragmentation smoothness. The original function had user selectable weights α,β to scale the effects of the gap distance and angle of the merge. The Fragmentation smoothness is the ratio of the path distance to the end point displacement. If the merged traces start forming a "U" shape or a loop it would result in a higher cost. A second alteration is to multiply the factors so that the outliers are further differentiated from the more probable traces. The resulting formula:
![C_2=\theta[\frac{d}{\Delta}]s](/mw/images/math/8/3/8/838dc6bcf55d56903864da4855c33cca.png)
accounts for the three factors of angle, gap distance, and smoothness of the trace.
Interpolate Large Gaps
Goal: Connect Large gaps that step 1 cannot simply connect by addition of a single cell Method: Larger gaps need new segments created,
new Trace Bits must be added,
smoothing operator.
- Curve fitting to find trend of:
- Direction
- Curvature
- Interpolation
- Extend the line
- Most probable vector
- Avoid creating edges
Branch Points
Goal: Detect and control Branching Method: Detect most probable intercepts,
Determination of main branch and child,
Type of branch point
- Distance maps
- Nearest neighbors (traces)
- Closest trace bits
- Angle of intercept
- Interpolation
Detect most probable intercepts: So far most of the methods I have evaluated or developed require information about the intensities in order to compute the most probable intercept. The reasoning behind this is the direction of the child branch does not give information about the intercept over long distances. In the short distance branching case, it is more acceptable to use the direction to figure out the interception point. The child branch would have to curve faster( over a shorter distance) if the direction of the branch was not in line with the main branch. In the case of a large gap between the main and child branch the child can curve slowly and still reach the main branch. This means that when there is a large gap there is more variation in the location of the intersection. So, to determine the proper intersection we can use the H(x) matrix listed in the features. I think when the gap is small( not sure what this is yet) we can just fill with a shortest distance line.
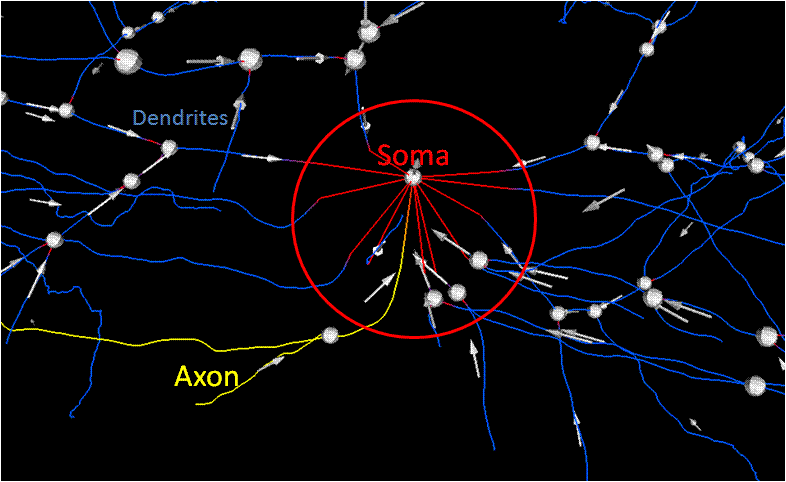
Soma Detection
Goal: Correspond processes with a soma Method: Segmentation of original data,
Localize the area to attach processes to soma,
Correct direction of traces
- Image intensity
- Blob segmentation
- Centroid
- Distance map
- Connectivity
- Connected components
- Localization of processes
Fragments
Goal: Removal of small traces that do not correspond to a process Method: Small traces removed,
Leftovers from splitting operators,
Line fragments that cannot be merged
- Lowest percentile of length
- Traces with no parents or children
- Type dependent
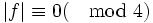 .
.
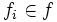 the
the 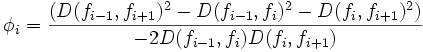 .
.
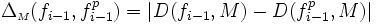 .
.
 is
is 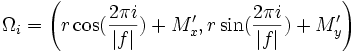 .
.
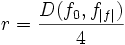 .
.
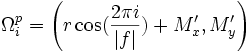
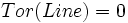 and
and