Object level association

From FarsightWiki
(Difference between revisions)
Jump to: navigation, search
(→Overview)
Line 1: Line 1:
−
In this page we give an overview of the distance map-based approach for defining object-level associations
+
In this page we give an overview of the distance map-based approach for defining object-level associations, instructions on how to run the association program and sample results
  
  
Line 52: Line 52:
  
 
== Running The Program ==
 
== Running The Program ==
−
to be added
+
A stand-alone executable for computing object-level association measurements is available in farsight. The program runs in two modes:
 +
1-associative rules defintion file is available
 +
2-no defition file is available
  
 
== Sample Output ==
 
== Sample Output ==
 
to be added
 
to be added

Revision as of 04:34, 3 May 2009

In this page we give an overview of the distance map-based approach for defining object-level associations, instructions on how to run the association program and sample results


Overview

We present a simple, yet general framework for object-level association between biological objects and/or elements present in the different channels of multi-channel images. The proposed object-level association framework assumes that any association rule is defined between two elements. The first one, which we call the reference element, is the segmented object (such as cells/nuclei) for which we want to quantify some associative relationships. The second element, which we call the target element, is a biologically meaningful element in a different channel. The target element does not have to be segmented or undergone under any kind of processing.

Two association examples are shown in Figure 1 below. In both examples, the reference element is a segmented cell nucleus. However, the target element in the first example (panel A) is a segmented blood vessel. Hence, association occurs between two segmented objects. In the second example (panel B), the target element is a molecular signal (yellow) that may surround some cell nuclei and available in a different channel.

Two association examples. Both examples use segmented nuclei as their reference elements but the target elements are a segmented blood vessel in (A), and a molecular signal from another channel (yellow) in (B).

An association rule is composed of two components. The first one defines the region of interest (ROI) associated with the reference elements and on which the associative measure is applied. The second component is an associative measure, which is a mathematical function defined on the regions of interest (ROI) of the reference elements, and used to quantify the associative relationship.


Defining The Region Of Interest

The region of interest (ROI) corresponding to an association rule is defined using a distance function. Starting from the edge points (segmentation boundary) 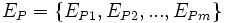{{E}_{P}}=\left\{ {{E}_{P1}},{{E}_{P2}},...,{{E}_{Pm}} \right\} of the reference element E, the distance function DE(x,y) computes the shortest signed Euclidean distance from a point (or in 3-D images) to the boundary points of the reference element:

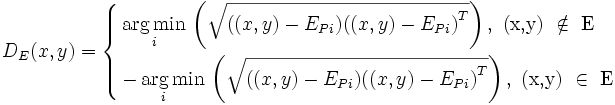{{D}_{E}}(x,y)=\left\{ \begin{align} & \underset{i}{\mathop{\arg \min }}\,\left( \sqrt{((x,y)-{{E}_{Pi}}){{((x,y)-{{E}_{Pi}})}^{T}}} \right),\text{ (x,y) }\notin \text{ E} \\ & \underset{i}{\mathop{-\arg \min }}\,\left( \sqrt{((x,y)-{{E}_{Pi}}){{((x,y)-{{E}_{Pi}})}^{T}}} \right),\text{ (x,y) }\in \text{ E} \\ \end{align} \right. where i = 1,2,...,m

Based on this distance function, the region of interest (RIO) is defined as a region with specific inside and outside (respectively negative and positive) distances. For example, 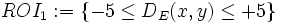RO{{I}_{1}}:=\left\{ -5\le {{D}_{E}}(x,y)\le +5 \right\} is the region of interest (ROI) that represent the region using an inside distance of 5 pixels/voxels from the boundary of the object (e.g cell nucleus) to 5 pixels/voxels outside. As another example, 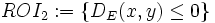RO{{I}_{2}}:=\left\{ {{D}_{E}}(x,y)\le 0 \right\} represents all the area enclosed by the object boundary.

Defining The Associative Measuer

As mentioned above, the associative measure is a mathematical function defined on the ROI of the reference element and used to quantify the association between the reference and the target elements. We represent the associative measure as a function that takes two input arguments ψROI(C,OP). The first one (C) is the target image (channel), and the second one (OP) refers to a mathematical operation to be used to quantify the association. Seeking simplicity and generality, our proposed associative measure can use any of the following different four operations:


\begin{align} & MIN:\text{ minimum value of the target element in the ROI of the reference element} \\ & MAX:\text{ maxmum value of the target element in the ROI of the reference element} \\ & AVERAGE:\text{ mean value of the target element in the ROI of the reference element} \\ & TOTAL:\text{ total of the target element in the ROI of the reference element} \\ \end{align}


Let the target element is present in image channel Ci, and let p be a point (2-D or 3-D) in Ci, then, the associative measure is defined as follows:


{{\psi }_{ROI}}\text{(}{{\text{C}}_{i}}\text{,OP)=}\left\{ \begin{align} & \underset{\text{p}\in \text{ROI}}{\mathop{\text{min}}}\,\text{(}{{\text{C}}_{\text{i}}}\text{(p)) , if OP=MIN} \\ & \underset{\text{p}\in \text{ROI}}{\mathop{\text{max}}}\,\text{(}{{\text{C}}_{\text{i}}}\text{(p)) , if OP=MAX} \\ & \int\limits_{\text{ROI}}{\omega \text{(p)}{{\text{C}}_{\text{i}}}\text{(p)dp , if OP=AVERAGE}} \\ & \int\limits_{\text{ROI}}{{{\text{C}}_{\text{i}}}\text{(p)dp , if OP=TOTAL}} \\ \end{align} \right.


where ω(.) is a weighting function that is uniformly distributed over ROI.

Running The Program

A stand-alone executable for computing object-level association measurements is available in farsight. The program runs in two modes: 1-associative rules defintion file is available 2-no defition file is available

Sample Output

to be added

Retrieved from "http://farsight-toolkit.ee.uh.edu/wiki/Object_level_association"
Personal tools