SuperEllipseTrace3D

From FarsightWiki
(Difference between revisions)
Jump to: navigation, search
(New page: This page presents automated methods for robust modeling and analysis of 3-D vascular images using a \textit{cylindroidal superellipsoid} to model localized segments of vasculature. The pr...)
 
Line 14: Line 14:
  
 
Superellipsoids are geometric modeling primitives first introduced
 
Superellipsoids are geometric modeling primitives first introduced
−
in early computer vision literature \cite{Barr:1981}.
+
in early computer vision literature [2].
 
Superellipsoids are expressed implicitly as:
 
Superellipsoids are expressed implicitly as:
  
−
<math>{equation}
+
<math>
−
\left(\left|x\right|^{\frac{2}{\epsilon_{2}}}+\left|y\right|^{\frac{2}{\epsilon_{2}}}\right)^{\frac{\epsilon_{2}}{\epsilon_{1}}}+\left|z\right|^{\frac{2}{\epsilon_{1}}}=1,\label{se}
+
\left(\left|x\right|^{\frac{2}{\epsilon_{2}}}+\left|y\right|^{\frac{2}{\epsilon_{2}}}\right)^{\frac{\epsilon_{2}}{\epsilon_{1}}}+\left|z\right|^{\frac{2}{\epsilon_{1}}}=1,
−
\end{equation}
+
 
 
</math>
 
</math>
  
Line 25: Line 25:
 
\epsilon=\left(\epsilon_{1},\epsilon_{2}\right) </math> control the
 
\epsilon=\left(\epsilon_{1},\epsilon_{2}\right) </math> control the
 
shape of the superellipsoid. To understand the role of
 
shape of the superellipsoid. To understand the role of
−
the shape parameters, first note that with <math>\epsilon_{1}=
+
the shape parameters, first note that with <math> \epsilon_{1}=
 
\epsilon_{2}=1 </math> equation 1 is simply an ellipsoid. With
 
\epsilon_{2}=1 </math> equation 1 is simply an ellipsoid. With
−
$\epsilon_{1}\leq 1$ and $\epsilon_{2}= 1$ the superellipsoid
+
<math>\epsilon_{1}\leq </math> and <math>\epsilon_{2}= 1</math> the superellipsoid
−
becomes a \textit{cylindroid}, i.e., the implicit surface bounds a
+
becomes a cylindroid, i.e., the implicit surface bounds a
−
convex region, where for constant $z$, the 2-D level curves are
+
convex region, where for constant <math>z</math>, the 2-D level curves are
−
elliptical. Setting $\epsilon_{1},\epsilon_{2}$ to other values
+
elliptical. Setting <math>\epsilon_{1},\epsilon_{2}</math> to other values
 
produces a variety of shapes including cuboids and pinched cuboids
 
produces a variety of shapes including cuboids and pinched cuboids
−
\cite{Barr:1981}. Since the goal in this work is to find an
+
[2]. Since the goal in this work is to find an
 
approximation to an elliptical cylinder, we will restrict our
 
approximation to an elliptical cylinder, we will restrict our
−
focus to cylindroidal forms. This means that $\epsilon_{2}$ in
+
focus to cylindroidal forms. This means that <math>\epsilon_{2}</math> in
−
equation (\ref{se}) is set to unity.
+
equation is set to unity.

Revision as of 23:42, 10 May 2009

This page presents automated methods for robust modeling and analysis of 3-D vascular images using a \textit{cylindroidal superellipsoid} to model localized segments of vasculature. The proposed vessel model has an explicit, low-order parameterization, allowing for joint estimation of boundary and centerline information, thereby approximating the medial axis of tubular structures. Further, this explicit parameterization provides a geometric framework for traversing vessels in a directed manner. Topological information like branch point location and connectivity can also be detected as a side effect. An M-estimators provide robust region-based statistics that are used to drive the superellipsoid toward a vessel boundary. The proposed methodology behaves quite well across scale-space, shows a high degree of insensitivity to adjacent structures and implicitly handles branching.


Contents


Local vascular modelling using Superellipse

The superellipsoid has an explicit low-order parameterization relating directly to the local pose of a vessel segment. Using this geometric information, it is straightforward to traverse entire vascular networks.Also, since the superellipsoid model furnishes joint estimates of the boundary and centerpoint of a vessel, the resulting traversal approximates the medial axis of each vessel in the vasculature. Another key advantage when using the superellipsoid model is that its local nature allows us to adapt vessel intensity estimates across different regions of the vasculature.

Also, since the superellipsoid model furnishes joint estimates of the boundary and centerpoint of a vessel, the resulting traversal approximates the medial axis of each vessel in the vasculature. Another key advantage when using the superellipsoid model is that its local nature allows us to adapt vessel intensity estimates across different regions of the vasculature.


Superellipsoids are geometric modeling primitives first introduced in early computer vision literature [2]. Superellipsoids are expressed implicitly as:

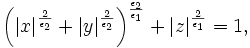
\left(\left|x\right|^{\frac{2}{\epsilon_{2}}}+\left|y\right|^{\frac{2}{\epsilon_{2}}}\right)^{\frac{\epsilon_{2}}{\epsilon_{1}}}+\left|z\right|^{\frac{2}{\epsilon_{1}}}=1,

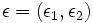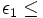where the parameters \epsilon=\left(\epsilon_{1},\epsilon_{2}\right) control the shape of the superellipsoid. To understand the role of the shape parameters, first note that with ε1 = ε2 = 1 equation 1 is simply an ellipsoid. With \epsilon_{1}\leq and ε2 = 1 the superellipsoid becomes a cylindroid, i.e., the implicit surface bounds a convex region, where for constant z, the 2-D level curves are elliptical. Setting ε1,ε2 to other values produces a variety of shapes including cuboids and pinched cuboids [2]. Since the goal in this work is to find an approximation to an elliptical cylinder, we will restrict our focus to cylindroidal forms. This means that ε2 in equation is set to unity.

Retrieved from "http://farsight-toolkit.ee.uh.edu/wiki/SuperEllipseTrace3D"
Personal tools