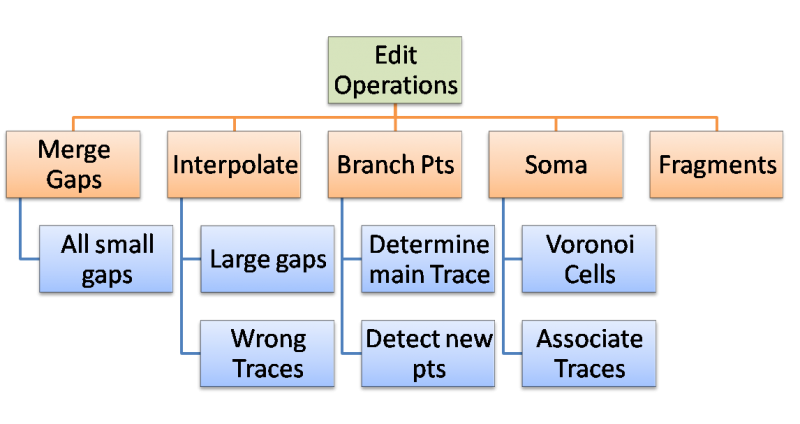
Trace Editor/Features

From FarsightWiki
(Difference between revisions)
Jump to: navigation, search
m (→Feature List)
(→Feature List)
Line 13: Line 13:
 
|-
 
|-
 
| Angle
 
| Angle
−
| Is the angle created between two traces normalized as vectors
+
| The angle created between two traces normalized as vectors
 
| <math> \theta = \arccos(\frac{v_1 \cdot v_2}{|v_1||v_2|}) </math>
 
| <math> \theta = \arccos(\frac{v_1 \cdot v_2}{|v_1||v_2|}) </math>
 
|-
 
|-
Line 41: Line 41:
 
|-
 
|-
 
| Curvature
 
| Curvature
−
| Considering using the Hessian matrix for checking branching point existence and interpolating the path.( still under consideration)
+
| The Hessian matrix for checking branching point existence and interpolating the path. (Still under consideration)
 
|<math>  
 
|<math>  
 
\left[\begin{array}{ccc}
 
\left[\begin{array}{ccc}
Line 50: Line 50:
 
|-
 
|-
 
| Parent  
 
| Parent  
−
| Considering nerves branching for a soma are a tree like structure a parent point can be used to find a cycle. If using only some point would be considered for the tree structure, not every voxel.( still under consideration)
+
| Considering nerves branching from the soma are a tree like structure, a parent point can be used to find a cycle.
 
|}
 
|}
  

Revision as of 15:36, 2 July 2009

Feature computation for Trace Editor

Feature List

Feature Description Equation or Variable
Gap Size Minimum distance between endpoints of two traces 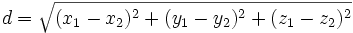d= \sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}
Angle The angle created between two traces normalized as vectors 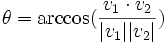\theta = \arccos(\frac{v_1 \cdot v_2}{|v_1||v_2|})
Path Length Total length along a trace, indicated by the size of the trace 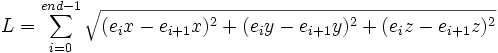L = \sum_{i=0}^{end - 1}\sqrt{(e_ix-e_{i+1}x)^2 + (e_iy-e_{i+1}y)^2+(e_iz-e_{i+1}z)^2}
Euclidean Distance Straight line distance between the endpoints of a trace 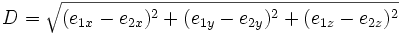D = \sqrt{(e_{1x}-e_{2x})^2 + (e_{1y}-e_{2y})^2+(e_{1z}-e_{2z})^2}
Fragmentation Smoothness Ratio of Path Length to Euclidean Distance[1] 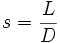s= \frac{L}{D}
Maximum Gap Distance The maximum distance between endpoints that can be merged Δ
Weights The weights are used in the cost algorithm α β
Cost Weighted scalar evaluating the merge 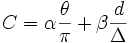C=\alpha\frac{\theta}{\pi}+\beta\frac{d}{\Delta}
Curvature The Hessian matrix for checking branching point existence and interpolating the path. (Still under consideration) \left[\begin{array}{ccc} f(x)_{xx}(X) + \frac{\alpha}{2}f_{yy}(X) + \frac{\alpha}{2}f_{zz}(X) & (1-\alpha)f_{xy}(X) & (1-\alpha)f_{xz}(X) \\ (1-\alpha)f_{xy}(X) & f_{yy}(X) + \frac{\alpha}{2}f(x)_{xx}(X) +\frac{\alpha}{2}f_{zz}(X) & (1-\alpha)f_{yz}(X) \\ (1-\alpha)f_{xz}(X) & (1-\alpha)f_{yz}(X) & f_{zz}(X) + \frac{\alpha}{2}f(x)_{xx}(X) +\frac{\alpha}{2}f_{yy}(X) \end{array} \right]
Parent Considering nerves branching from the soma are a tree like structure, a parent point can be used to find a cycle.

Algorithms

The algorithms suggested are used to control the editing process allowing for rule based cluster editing. The Goal is to complete group editing in five steps.

Proposed steps of editing
1: Merge Small Gaps
Goal: Create longest continuous trace segments by merging close endpoints
Methods: Nearest neighbors  (Closest end points), 
Rejection based on conflicts and thresholds
  • Minimal distance between end points
    • Angle between traces- The angle is measured between the two traces by computing the norm of their vectors and the dot product.
      The equation is: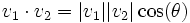 v_1 \cdot v_2 = |v_1||v_2| \cos(\theta) which when solved for θ is: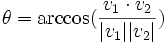 \theta = \arccos(\frac{v_1 \cdot v_2}{|v_1||v_2|})
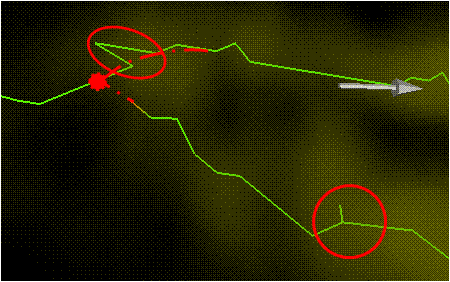
    • Path length- If the end points are not the best fit for the merge this is when path length is considered. An example of this would be a peak in the neurite on completion the given merge. An example if given in an image in this section. This is also discussed in large gaps being that in the large gap case these type of error cause more of a problem. a sharp change in a neurite in a subsection prior to the end point would indicate this error. Merging at the sharp direction change( especially in the small gap case) can alleviate the neurite of peaks.
    • Gap distance is too large- If the distance between the two points e1, e2 is greater then the excepted distance for a small gap then they will not be considered. This is tested prior to computing the angular difference due to the expense of computing angles. Between this case and the angular case we have a similar metric to the cost function in "Automated Three-Dimensional Tracing of Neurons in Confocal and Brightfield Images"; however, the conditions under which we check for small gaps is when there are only two end points to be merged
    • Consider possibility of loops Even though this might not be possible in the 3D case, if we were to use a 2D projection of the picture there might be a situation where multiple breaks might end in a loop. consider the cross sectioning of two neurites. A gap at anyone of the intersections could cause connection problems. This matter on the cost function this could mean a loop will form. This formation might not be correct, but I think we should at least consider it.
Two neurites that might cause a problem for the merging minor gaps algorithm.
  • Another trace is a better fit (Cost Function)
    • Smallest gap
    • Better Angular alignment
  • "Bad merge"
    • The merge causes corners
    • Needs to be smoothed 
2: Interpolate Large Gaps
Goal: Connect Large gaps that step 1 cannot  simply connect by addition of a  single cell
Method: Larger gaps need new segments created, 
new Trace Bits must be added, 
smoothing operator.
Example showing how Merging and branching are interconnected. The Merging that creates sharp turns needs to be smoothed. The Traces need to create a new branch point and trace bits to interpolate the original
  • Curve fitting to find trend of:
    • Direction
    • Curvature
  • Interpolation
    • Extend the line
    • Most probable vector
    • Avoid creating edges

path of the branch. 

3: Branch Points
Goal: Detect and control Branching
Method: Detect most probable intercepts, 
Determination of main branch and child, 
Type of branch point
  • Distance maps
    • Nearest neighbors (traces)
    • Closest trace bits
  • Angle of intercept
  • Interpolation 
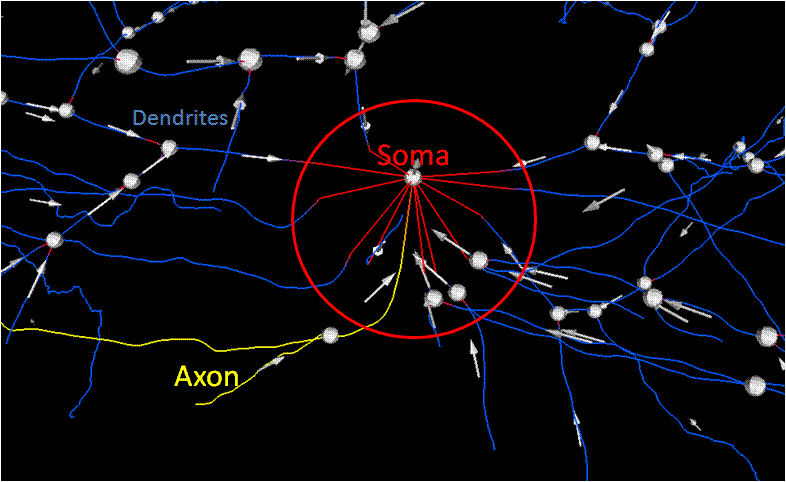
4: Soma Detection
Goal: Correspond processes with a soma
Method: Segmentation of original data, 
Localize the area to attach processes to soma, 
Correct direction of traces
  • Image intensity
  • Blob segmentation
  • Centroid
  • Distance map
  • Connectivity
    • Connected components
    • Localization of processes
Illustration of how the processes should be connected to a soma(shown in red).
The Dendrites are shown in blue, where the axon is shown in yellow.
5: Fragments
Goal: Removal of small traces that do not correspond to a process
Method: Small traces removed, 
Leftovers from splitting operators, 
Line fragments that cannot be merged
  • Lowest percentile of length
    • Traces with no parents or children
    • Type dependent

References

Template:Reflist


Cite error: <ref> tags exist, but no <references/> tag was found
Retrieved from "http://farsight-toolkit.ee.uh.edu/wiki/Trace_Editor/Features"
Personal tools