Dendritic Spine Segmentation
(→Segmenting Dendritic Spines From 3D Confocal Microscopy Images) |
|||
| Line 1: | Line 1: | ||
| − | ==Segmenting Dendritic Spines From 3D Confocal Microscopy Images== | + | [[==Segmenting Dendritic Spines From 3D Confocal Microscopy Images== |
[[Image:MIN_spine1-deconvolved.png]] | [[Image:MIN_spine1-deconvolved.png]] | ||
| Line 8: | Line 8: | ||
==Dendritic Spine Basics== | ==Dendritic Spine Basics== | ||
| − | Previously considered insignificant artifacts on the dendritic shaft, the thorn-like protrusions of neuronal membranes first gained attention with Ramon y Cajal’s (1852-1934) novel interpretations of brain tissue images in 1888. Since then, not only the name ''spines'' has been retained, but also much of Cajal’s neural spine hypotheses | + | Previously considered insignificant artifacts on the dendritic shaft, the thorn-like protrusions of neuronal membranes first gained attention with Ramon y Cajal’s (1852-1934) novel interpretations of brain tissue images in 1888. Since then, not only the name ''spines'' has been retained, but also much of Cajal’s neural spine hypotheses - dflp , garcia- Despite the primitiveness of his microscope and techniques, Cajal’s elucidations have laid the foundations of modern neurology(Hamburger 1980). |
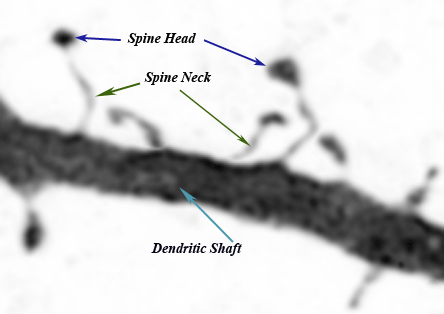
Spines arise from the neuronal membrane at the soma, dendrites, or the axon hillock | Spines arise from the neuronal membrane at the soma, dendrites, or the axon hillock | ||
in tiny structures and in different directions (Harris, Jensen et al. 1992; Nimchinsky, Sabatini et al. 2002). Their morphologies are quite diverse but are broadly qualified by | in tiny structures and in different directions (Harris, Jensen et al. 1992; Nimchinsky, Sabatini et al. 2002). Their morphologies are quite diverse but are broadly qualified by | ||
| Line 30: | Line 30: | ||
==Our Methodology== | ==Our Methodology== | ||
In our algorithm we model the dendritic shaft as a tube-like structure of varying diameter in noise studded with spines, filopodia and/or varicosities. Automated tracing of the dendritic backbone is accomplished by a previously developed algorithm that fits superellipsoids robustly and estimates the local intensity surrounding them. Once this is done, the spines are initially detected by first extracting the surrounding regions that deviate from the tubular geometry. A generalized likelihood ratio test is used to determine whether the initially segmented region represents a spine or just imaging noise. Because spine sizes are close to the achievable image resolution, and fluorescent marker intensity fluctuates within the spine, many spines appear fragmented and/or disconnected from the dendrite and thus require further analysis. Our algorithm sports a novel approach that reconnects apparently detached spines and calculates accurately the spine length using Fast Marching. The spine head, total volume, protrusion from the dendrite surface are features we evaluate for further discriminant analysis. | In our algorithm we model the dendritic shaft as a tube-like structure of varying diameter in noise studded with spines, filopodia and/or varicosities. Automated tracing of the dendritic backbone is accomplished by a previously developed algorithm that fits superellipsoids robustly and estimates the local intensity surrounding them. Once this is done, the spines are initially detected by first extracting the surrounding regions that deviate from the tubular geometry. A generalized likelihood ratio test is used to determine whether the initially segmented region represents a spine or just imaging noise. Because spine sizes are close to the achievable image resolution, and fluorescent marker intensity fluctuates within the spine, many spines appear fragmented and/or disconnected from the dendrite and thus require further analysis. Our algorithm sports a novel approach that reconnects apparently detached spines and calculates accurately the spine length using Fast Marching. The spine head, total volume, protrusion from the dendrite surface are features we evaluate for further discriminant analysis. | ||
| + | ===Spine Ring Detector=== | ||
| + | ===Spine Candidates=== | ||
| + | ===Geodesic Tractography=== | ||
| + | ===Feature Extraction=== | ||
| + | ===Edit-Based Validation Using Farsight=== | ||
| + | ===References=== | ||
| + | <references/> | ||
| + | <ref name="dflp">DeFelipe, J., Ed. (1999). Cajal. The MIT encyclopedia of the cognitive sciences. Cambridge, Mass., MIT Press </ref>. | ||
| + | <ref name="garcia">Garcia-Lopez, P., V. Garcia-Marin, et al. (2006). "Three-dimensional reconstruction and quantitative study of a pyramidal cell of a Cajal histological preparation." J Neurosci 26(44): 11249-52 </ref> | ||
Revision as of 17:48, 24 April 2009
[[==Segmenting Dendritic Spines From 3D Confocal Microscopy Images==
Dendritic spines are key to understanding brain cognition and memory as well as drug interaction effects. Their significance has increased in the past decade with advances in 3-D fluorescence microscopy imaging especially for time-lapse analysis (4-D image data) in the context of pre-clinical studies. Segmenting spines is necessary to achieve accurate quantification across several snapshots.
Contents |
Dendritic Spine Basics
Previously considered insignificant artifacts on the dendritic shaft, the thorn-like protrusions of neuronal membranes first gained attention with Ramon y Cajal’s (1852-1934) novel interpretations of brain tissue images in 1888. Since then, not only the name spines has been retained, but also much of Cajal’s neural spine hypotheses - dflp , garcia- Despite the primitiveness of his microscope and techniques, Cajal’s elucidations have laid the foundations of modern neurology(Hamburger 1980). Spines arise from the neuronal membrane at the soma, dendrites, or the axon hillock in tiny structures and in different directions (Harris, Jensen et al. 1992; Nimchinsky, Sabatini et al. 2002). Their morphologies are quite diverse but are broadly qualified by the head volume and neck diameter. The most commonly used nomenclature categorizes them into(Harris, Jensen et al. 1992; Nimchinsky, Sabatini et al. 2002):
- stubby, closely attached to the dendrite with no obvious neck
- mushroom, has a narrow neck and a large head
- thin, narrow neck and elongated stem with no head
- bifurcated or branched, similar to the mushroom but with a split head.
Fiala et. al.(Fiala and Harris 1999) indicate the dominance of these four types, especially thin-shaped spines, but nevertheless describe a continuum of length and neck deformations. Moreover, specific neurons exhibit additional spine types such as crook thorn and the gemmules.
Significance and 3D Imaging
Topics such as dendritic spine properties (shape, size, distribution, density, …), plasticity, their relationship with the neuronal tree and their role within the synapse are the subject of ongoing research(Yuste and Bonhoeffer 2004; Garcia-Lopez, Garcia-Marin et al. 2006). The computational functionality of the neural dendrite and the role of the spine as the smallest subunit is analyzed in (Sidiropoulou, Pissadaki et al. 2006). Although the complete functions of spines are still not well understood(Yuste and Bonhoeffer 2004), it is widely believed that spines are responsible for information exchange at the synapse. Numerous studies examine dendritic spine correlation with memory(Yuste and Bonhoeffer 2001), cognition and related disorders such as Alzheimer’s Disease(Akram, Christoffel et al. 2007) and fragile X syndrome(Comery, Harris et al. 1997). In recent years, advances in 3D imaging technologies have contributed to increased attention towards investigating spinal structure, development, as well as drug interaction(Harris, Jensen et al. 1992; Nimchinsky, Sabatini et al. 2002; Trachtenberg, Chen et al. 2002; Potter 2005) Age-related spine changes were investigated by (Duan, Wearne et al. 2003) using 3-D confocal images although spine counts were done on 1µm-separated 2-D slices. A recent study on human brain tissue(Akram, Christoffel et al. 2007) found a strong correlation between cognitive decline due to Alzheimer disease and dendritic spine loss. In (Johnson and Ouimet 2004) 3D imaging was used for spine and filopodia length measurements at different time points in order to assess certain drug interactions (protein inhibitors) on spine growth.
Our Methodology
In our algorithm we model the dendritic shaft as a tube-like structure of varying diameter in noise studded with spines, filopodia and/or varicosities. Automated tracing of the dendritic backbone is accomplished by a previously developed algorithm that fits superellipsoids robustly and estimates the local intensity surrounding them. Once this is done, the spines are initially detected by first extracting the surrounding regions that deviate from the tubular geometry. A generalized likelihood ratio test is used to determine whether the initially segmented region represents a spine or just imaging noise. Because spine sizes are close to the achievable image resolution, and fluorescent marker intensity fluctuates within the spine, many spines appear fragmented and/or disconnected from the dendrite and thus require further analysis. Our algorithm sports a novel approach that reconnects apparently detached spines and calculates accurately the spine length using Fast Marching. The spine head, total volume, protrusion from the dendrite surface are features we evaluate for further discriminant analysis.
Spine Ring Detector
Spine Candidates
Geodesic Tractography
Feature Extraction
Edit-Based Validation Using Farsight
References
Cite error:
<ref> tags exist, but no <references/> tag was found