SuperEllipseTrace3D

From FarsightWiki

Revision as of 02:42, 11 May 2009 by Mukhea (Talk | contribs)

(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)

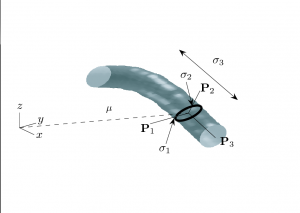
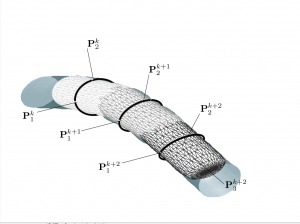
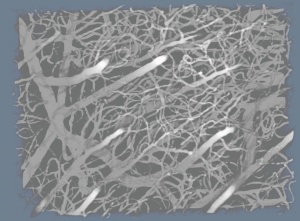
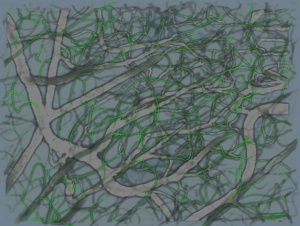
This page presents automated methods for robust modeling and analysis of 3-D vascular images using a \textit{cylindroidal superellipsoid} to model localized segments of vasculature. The proposed vessel model has an explicit, low-order parameterization, allowing for joint estimation of boundary and centerline information, thereby approximating the medial axis of tubular structures. Further, this explicit parameterization provides a geometric framework for traversing vessels in a directed manner. Topological information like branch point location and connectivity can also be detected as a side effect. An M-estimators provide robust region-based statistics that are used to drive the superellipsoid toward a vessel boundary. The proposed methodology behaves quite well across scale-space, shows a high degree of insensitivity to adjacent structures and implicitly handles branching.

Local vascular modelling using Superellipse

The superellipsoid provides the basis for a simple shape model that describes localized vessel segments. It has an explicit low-order parameterization relating directly to the local pose of a vessel segment. Using this geometric information, it is straightforward to traverse entire vascular networks.Also, since the superellipsoid model furnishes joint estimates of the boundary and centerpoint of a vessel, the resulting traversal approximates the medial axis of each vessel in the vasculature. Another key advantage when using the superellipsoid model is that its local nature allows us to adapt vessel intensity estimates across different regions of the vasculature.

Also, since the superellipsoid model furnishes joint estimates of the boundary and centerpoint of a vessel, the resulting traversal approximates the medial axis of each vessel in the vasculature. Another key advantage when using the superellipsoid model is that its local nature allows us to adapt vessel intensity estimates across different regions of the vasculature.

Figure1: Shows the boundary of a superellispoid while the shape parameter

ε 1

is varied between 1.0 and 0.25 and

ε 2

is set to 1.

Superellipsoids are geometric modeling primitives first introduced in early computer vision literature [2]. Superellipsoids are expressed implicitly as:

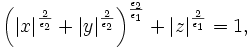
$\left(\left|x\right|^{\frac{2}{\epsilon_{2}}}+\left|y\right|^{\frac{2}{\epsilon_{2}}}\right)^{\frac{\epsilon_{2}}{\epsilon_{1}}}+\left|z\right|^{\frac{2}{\epsilon_{1}}}=1,$

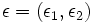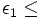where the parameters $\epsilon=\left(\epsilon_{1},\epsilon_{2}\right)$ control the shape of the superellipsoid. To understand the role of the shape parameters, first note that with $ε 1 = ε 2 = 1$ equation 1 is simply an ellipsoid. With $\epsilon_{1}\leq$ and $ε 2 = 1$ the superellipsoid becomes a cylindroid, i.e., the implicit surface bounds a convex region, where for constant $z$ , the 2-D level curves are elliptical. Setting $ε 1,ε 2$ to other values produces a variety of shapes including cuboids and pinched cuboids [2]. Since the goal in this work is to find an approximation to an elliptical cylinder, we will restrict our focus to cylindroidal forms. This means that $ε 2$ in equation is set to unity.

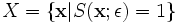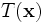Starting with a set of points in the set $X=\left\{\mathbf{x}|S(\mathbf{x};\epsilon)=1\right\}$ ( $ε$ is fixed), a transformation given by $T(\mathbf{x})=\mathbf{R}({\phi})\mathbf{D}({\sigma})\mathbf{x}+{\mu}$ can be performed. This transformation preserves orthogonality of the local coordinate frame while allowing for anisotropic scaling. 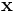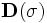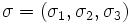The action of $T(\mathbf{x})$ is to first scale $\mathbf{x}$ by $\mathbf{D}({\sigma})$ , which is a $3\times 3$ matrix with scale parameters ${\sigma}=\left(\sigma_{1},\sigma_{2},\sigma_{3}\right)$ on the diagonal. 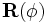Then, a rotation is performed via the $3\times 3$ matrix $\mathbf{R}({\phi})$ with three degrees of freedom that is parameterized by $φ$ . 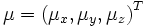Finally, a shift via ${\mu}=\left(\mu_{x},\mu_{y},\mu_{z}\right)^{T}$ is performed. 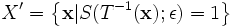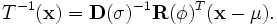This transformation leads to a new superellipsoid defined by the set having 10 degrees of freedom in 3D, $X'=\left\{\mathbf{x}|S(T^{-1}(\mathbf{x});\epsilon)=1\right\}$ , where, $T^{-1}(\mathbf{x})=\mathbf{D}({\sigma})^{-1}\mathbf{R}({\phi})^{T}(\mathbf{x}-{\mu}).$

Vessel Model Formulation

When estimating the superellipsoid model parameters we will assume that a vessel segment consists of two piece-wise constant regions with intensities denoted $I F$ for foreground and $I B$ for background and that the vessel boundary separating these regions is well-modeled by a superellipsoid. The local vessel intensities are modeled using a homogeneous grayscale appearance model as

$V(\mathbf{x};{\theta})= I_{B}-(I_{B}-I_{F})\times 1_{\left[S(\mathbf{x},{\beta})<1\right]},$

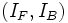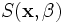where ${\theta}=\left(I_{F},I_{B},{\beta}\right)$ is the full parameter set of the superellipsoid vessel model. This includes the intensity parameters $\left(I_{F},I_{B}\right)$ that describe the foreground and background intensities respectively, as well as the underlying parameters of the superellipsoid shape model, i.e., $S(\mathbf{x},{\beta})$ . The notation $1_{\left[\cdot\right]}$ denotes an indicator function that evaluates to one on the set specified in the subscript and is zero elsewhere.

The strategy for maximizing equation is to alternate between estimating the intensity parameters and then updating the boundary using a gradient search. The following two subsections will detail each step.

Figure2:

Figure3:

Figure4:

Figure5:

SuperEllipseTrace3D

Contents

Local vascular modelling using Superellipse

Views

Personal tools

Navigation

Search

Toolbox